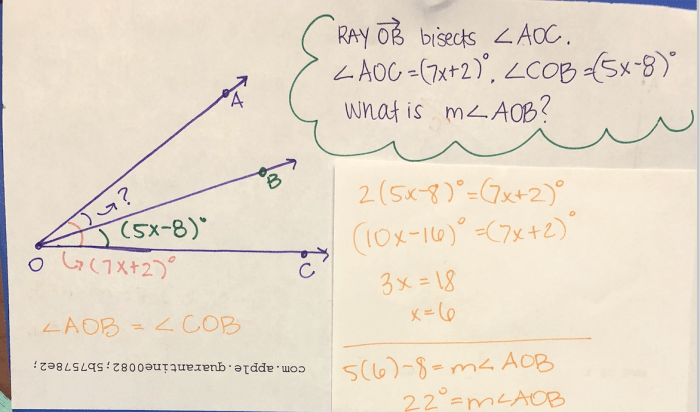Practice a perpendicular and angle bisectors – Practice Perpendicular and Angle Bisectors introduces readers to the fundamental concepts and applications of these geometric tools. Delving into the world of geometry, this comprehensive guide unravels the significance of perpendicular bisectors and angle bisectors, empowering individuals to confidently navigate the intricacies of geometric constructions and problem-solving.
As we embark on this geometric journey, we will explore the techniques for constructing perpendicular bisectors and angle bisectors using compasses and straightedges, unraveling their unique properties and applications. Through real-world examples, we will witness the practical relevance of these geometric concepts, solidifying our understanding of their importance in various fields.
Perpendicular Bisectors
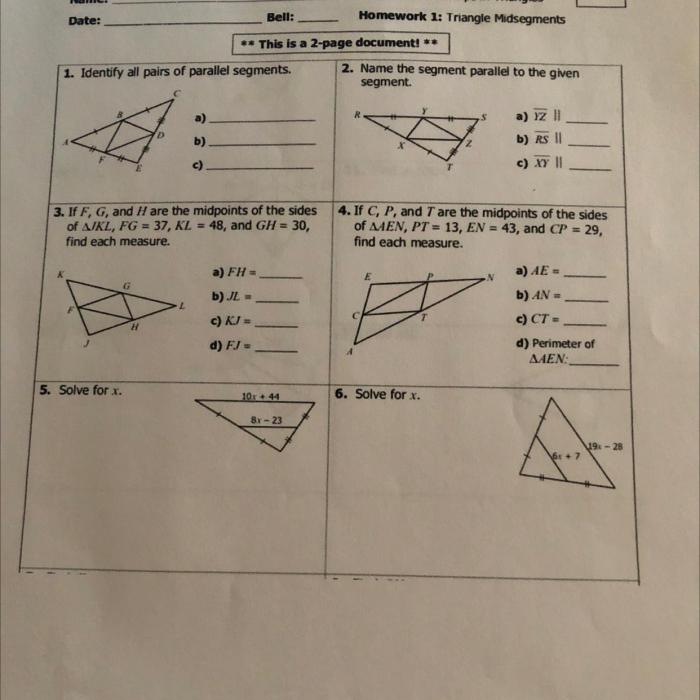
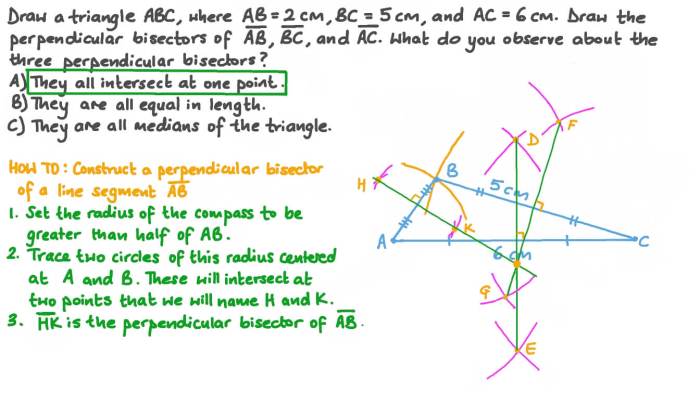
A perpendicular bisector is a line that passes through the midpoint of a line segment and is perpendicular to it. Perpendicular bisectors are important in geometry because they can be used to find the midpoint of a line segment, to construct perpendicular lines, and to divide angles into two equal parts.
Constructing Perpendicular Bisectors
To construct a perpendicular bisector using a compass and straightedge, follow these steps:
- Draw the line segment.
- Place the compass point on one endpoint of the line segment and draw an arc that intersects the line segment at two points.
- Without changing the compass setting, place the compass point on the other endpoint of the line segment and draw another arc that intersects the first arc at two points.
- Draw a line through the two points of intersection. This line is the perpendicular bisector of the line segment.
Properties of Perpendicular Bisectors
The perpendicular bisector of a line segment has the following properties:
- It passes through the midpoint of the line segment.
- It is perpendicular to the line segment.
- It divides the line segment into two equal parts.
Applications of Perpendicular Bisectors, Practice a perpendicular and angle bisectors
Perpendicular bisectors have many applications in real-world scenarios, including:
- Finding the midpoint of a line segment
- Constructing perpendicular lines
- Dividing angles into two equal parts
Angle Bisectors: Practice A Perpendicular And Angle Bisectors
An angle bisector is a line that divides an angle into two equal parts. Angle bisectors are important in geometry because they can be used to find the measure of an angle, to construct perpendicular lines, and to divide line segments into two equal parts.
Constructing Angle Bisectors
To construct an angle bisector using a compass and straightedge, follow these steps:
- Draw the angle.
- Place the compass point on the vertex of the angle and draw an arc that intersects the two sides of the angle at two points.
- Without changing the compass setting, place the compass point on one side of the angle and draw an arc that intersects the first arc at two points.
- Draw a line through the two points of intersection. This line is the angle bisector.
Properties of Angle Bisectors
The angle bisector of an angle has the following properties:
- It passes through the vertex of the angle.
- It divides the angle into two equal parts.
- It is perpendicular to the line segment that connects the two endpoints of the angle.
Applications of Angle Bisectors
Angle bisectors have many applications in real-world scenarios, including:
- Finding the measure of an angle
- Constructing perpendicular lines
- Dividing line segments into two equal parts
FAQ Overview
What is a perpendicular bisector?
A perpendicular bisector is a line that intersects a line segment at its midpoint and forms a right angle with it.
What is an angle bisector?
An angle bisector is a line that divides an angle into two equal parts.
How do you construct a perpendicular bisector?
To construct a perpendicular bisector, place the compass point on one endpoint of the line segment. Adjust the compass to a radius greater than half the length of the line segment. Draw an arc that intersects the line segment at two points.
Repeat this process from the other endpoint. The intersection of the two arcs is the midpoint of the line segment. Draw a line through the midpoint perpendicular to the line segment to construct the perpendicular bisector.